 丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼侾俇
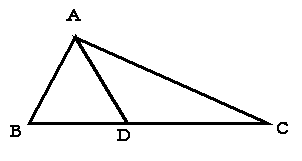
丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼侾俇 偱丆俛俢偲俢俠偺挿偝偺斾偼係丗俆偱偡丅偙偺偲偒丆嶰妏宍俙俛俠偺柺愊偼丂丂丂丂
偱丆俛俢偲俢俠偺挿偝偺斾偼係丗俆偱偡丅偙偺偲偒丆嶰妏宍俙俛俠偺柺愊偼丂丂丂丂 偱偡丅
偱偡丅
柺愊偲斾侾 |
 塃偺恾偺俆偮偺嶰妏宍偺柺愊偑丆偡傋偰摍偟偄偙偲偑傢偐傝傑偡偐丠
塃偺恾偺俆偮偺嶰妏宍偺柺愊偑丆偡傋偰摍偟偄偙偲偑傢偐傝傑偡偐丠
 偦傟傪塃偺恾偺傛偆偵偔偭偮偗傞偲丆
偦傟傪塃偺恾偺傛偆偵偔偭偮偗傞偲丆

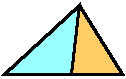 丂側傜俷俲偱偡偑丆
丂側傜俷俲偱偡偑丆 丂傗丂
丂傗丂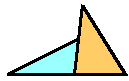 丂偼偄偗傑偣傫丅
丂偼偄偗傑偣傫丅
 丂偺傛偆偵偐偨傓偄偰偄傞応崌偱傕丄捀揰偐傜慄傪傂偄偰偄傑偡偹丅
丂偺傛偆偵偐偨傓偄偰偄傞応崌偱傕丄捀揰偐傜慄傪傂偄偰偄傑偡偹丅
 丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼侾俇 丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼侾俇 偱丆俛俢偲俢俠偺挿偝偺斾偼係丗俆偱偡丅偙偺偲偒丆嶰妏宍俙俛俠偺柺愊偼丂丂丂丂 偱丆俛俢偲俢俠偺挿偝偺斾偼係丗俆偱偡丅偙偺偲偒丆嶰妏宍俙俛俠偺柺愊偼丂丂丂丂 偱偡丅 偱偡丅
|
| 栤戣侾偺摎偊 | 俁俇 |
|
| 栤戣侾偺夝愢 |  丂丂 丂丂 丂丂丂1/5 丂丂丂1/5 |
|
 |
俛俢偲俢俠偺挿偝偺斾偑係丗俆偱偡偐傜丆
嶰妏宍俙俛俢偲嶰妏宍俙俢俠偺柺愊偺斾傕係丗俆偱偡丅 |
|
| 曗廩栤戣 | (丂丂偺偲偙傠偵儅僂僗傪嬤偯偗傞偲丄摎偊偑昞帵偝傟傑偡丅) | |
 丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼俁侽 丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼俁侽 偱丆俛俢偲俢俠偺挿偝偺斾偼俇丗侾侾偱偡丅偙偺偲偒丆嶰妏宍俙俛俠偺柺愊偼丂丂丂丂 偱丆俛俢偲俢俠偺挿偝偺斾偼俇丗侾侾偱偡丅偙偺偲偒丆嶰妏宍俙俛俠偺柺愊偼丂丂丂丂 偱偡丅 偱偡丅
|
||
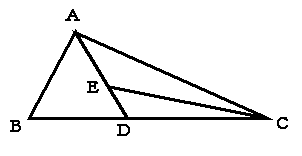 丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼俀係 丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼俀係 偱丆嶰妏宍俙俠俤偺柺愊偼俀侽 偱丆嶰妏宍俙俠俤偺柺愊偼俀侽 偱偡丅傑偨丆俙俤偲俤俢偺挿偝偺斾偼俆丗俁偱偡丅 偱偡丅傑偨丆俙俤偲俤俢偺挿偝偺斾偼俆丗俁偱偡丅
丂偙傟偵偮偄偰丆師偺栤偄偵摎偊側偝偄丅 (1)丂嶰妏宍俤俢俠偺柺愊偼丂丂丂丂  偱偡丅 偱偡丅
(2)丂俛俢偲俢俠偺挿偝偺斾偼丆丂丂丂丂丗丂丂丂丂偱偡丅 |
| 栤戣俀偺摎偊 | ||
| 栤戣俀偺夝愢 |  丂丂 丂丂 丂丂丂1/7 丂丂丂1/7 |
|
 | -->
(1)丂僀 偲 僂 偺柺愊偺斾偼丆
丂俙俤丗俤俢偲摨偠偱偡偐傜俆丗俁偱偡丅 |
|
| 曗廩栤戣 | (丂丂偺偲偙傠偵儅僂僗傪嬤偯偗傞偲丄摎偊偑昞帵偝傟傑偡丅) | |
 丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼俇侽 丂塃偺恾偱丆嶰妏宍俙俛俢偺柺愊偼俇侽 偱丆嶰妏宍俙俠俤偺柺愊偼係俆 偱丆嶰妏宍俙俠俤偺柺愊偼係俆 偱偡丅傑偨丆俙俤偲俤俢偺挿偝偺斾偼俁丗俀偱偡丅 偱偡丅傑偨丆俙俤偲俤俢偺挿偝偺斾偼俁丗俀偱偡丅
丂偙傟偵偮偄偰丆師偺栤偄偵摎偊側偝偄丅 (1)丂嶰妏宍俤俢俠偺柺愊偼丂丂丂丂  偱偡丅 偱偡丅
(2)丂俛俢偲俢俠偺挿偝偺斾偼丆丂丂丂丂丗丂丂丂丂偱偡丅 |
||
|
| 栤戣俁偺摎偊 | (1)係丗俁丂丂丂(2)俆丗俁丂丂丂(3)1俀 | |||
| 栤戣俁偺夝愢 |  丂丂 丂丂 丂丂丂1/6 丂丂丂1/6 |
|||
 |
(1)丂俙俤丗俤俢偼丆傾丗僀偲摍偟偔側傝傑偡偐傜丆
丂俀侽丗侾俆亖係丗俁丂偲側傝傑偡丅 |
|||
| 曗廩栤戣 | (丂丂偺偲偙傠偵儅僂僗傪嬤偯偗傞偲丄摎偊偑昞帵偝傟傑偡丅) | |||
| ||||