 右の図のように,AD:DB=3:5,AE:EC=1:1で,
右の図のように,AD:DB=3:5,AE:EC=1:1で,
三角形ADEの面積が12
 のとき,
三角形ABCの面積を求めなさい。
のとき,
三角形ABCの面積を求めなさい。
面積と比2 |
 右の図のように,AD:DB=3:5,AE:EC=1:1で,
右の図のように,AD:DB=3:5,AE:EC=1:1で,
 のとき,
三角形ABCの面積を求めなさい。
のとき,
三角形ABCの面積を求めなさい。
| 解説 |   1/19 1/19 |
|
 |
この問題では, の形がありません。そのときは,補助線をひいて, の形がありません。そのときは,補助線をひいて, の形をつくりましょう。 の形をつくりましょう。
|
|
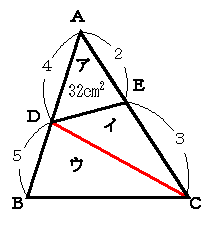
 右の図の三角形ADEの面積は32 右の図の三角形ADEの面積は32 です。このとき,四角形DBCEの面積は です。このとき,四角形DBCEの面積は  です。 です。
|
| 問題1の答え |  |
|
| 問題1の解説 |   1/14 1/14 |
|
 | -->
= 解き方1 =
左の図の赤い線のように補助線をひくと,ア:イ=2:3 です。 |
|
| 補充問題 | ( のところにマウスを近づけると、答えが表示されます。) | |
 右の図の三角形ADEの面積は80 右の図の三角形ADEの面積は80 です。このとき,四角形DBCEの面積は です。このとき,四角形DBCEの面積は  です。 です。
|
||
 右の図の三角形ABCで,点Eは辺BCの真ん中の点です。 右の図の三角形ABCで,点Eは辺BCの真ん中の点です。三角形DBEの面積が10  ,四角形ADECの面積が18 ,四角形ADECの面積が18 のとき,AD:DB= : です。 のとき,AD:DB= : です。
|
| 問題2の答え | 2:5 | |
| 問題2の解説 |   1/9 1/9 |
|
 |
この問題は,左の図の赤い線のように,DからCまで補助線をひくと,解きやすくなります。
Eは辺BCの真ん中なので,アとイの面積も同じです。 アの面積は10  ですから,イの面積も10 ですから,イの面積も10 です。 です。
よって,アイの面積は,10×2=20(  )になり, )になり,
ウの面積は,18−10=8(  )になります。 )になります。
 求めたいのは,AD:DBです。 求めたいのは,AD:DBです。
これは,ウ:アイと同じです。 ウの面積は8  ,アイの面積は20 ,アイの面積は20 でしたから, でしたから,
AD:DB=ウ:アイ=8:20=2:5 となります。 |
|
| 補充問題 | ( のところにマウスを近づけると、答えが表示されます。) | |
 右の図の三角形ABCで,BE:EC=4:5です。 右の図の三角形ABCで,BE:EC=4:5です。三角形DBEの面積が56  ,四角形ADECの面積が124 ,四角形ADECの面積が124 のとき,AD:DB= : です。 のとき,AD:DB= : です。
|
||