平面図形と比１

問題番号がボタンになっています。クリックすると答えと解説が表示されます。

  左図のような台形ＡＢＣＤがあります。この図で、ＢＥ：ＥＤの長さの比を求めなさい。また、ＡＤの長さを求めなさい。


問題１の答え１６：２５、５０ｃｍ
解説 　　　　  1/13

左図のような四角形において、
ア：イ　の長さの比は、
補充問題(　　のところにマウスを近づけると、答えが表示されます。)

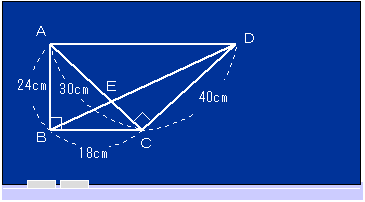左図のような台形ＡＢＣＤがあります。この図で、ＢＥ：ＥＤの長さの比は　　　です。また、ＡＤの長さは　　　cmです。






  左図で、ＡＣの長さは４８ｃｍで、三角形ＡＢＤと三角形ＢＣＤの面積の比は５：３です。このとき、ＡＥの長さは何ｃｍですか。


問題２の答え30ｃｍ
解説 　　　　  1/6

左図の四角形において、
ア：イを求めるときは、
補充問題(　　のところにマウスを近づけると、答えが表示されます。)

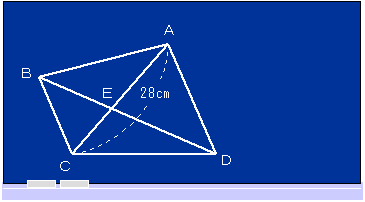左図で、ＡＣの長さは２８ｃｍで、三角形ＡＢＤと三角形ＢＣＤの面積の比は４：３です。このとき、ＡＥの長さは　　　ｃｍです。






  左図の四角形ＡＢＣＤは１辺が２０ｃｍの正方形で、Ｅ、Ｆはそれぞれ辺ＡＢ、辺ＡＤの真ん中の点です。
(1)　ＥＧ：ＧＣを求めなさい。
(2)　三角形ＧＢＣの面積は何ですか。
(3)　ＢＧ：ＧＦを求めなさい。


問題３の答え(1)　１：４　　　　(2)　８０　　　　(３)　２：３
解説 　　　　  1/13

まず、(1)の問題です。
左図の四角形で、ア：イの長さの比を求めたいときは、灰色の三角形と、ピンク色の三角形の面積の比を求めればよいのです。
補充問題(　　のところにマウスを近づけると、答えが表示されます。)

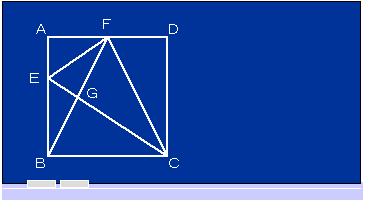左図の四角形ＡＢＣＤは１辺が１２ｃｍの正方形で、Ｅは辺ABを３等分する点の１つで、Ｆは辺ＡＤの真ん中の点です。
(1)　ＥＧ：ＧＣは　　　：　　　です。
(2)　三角形ＧＢＣの面積は　　　です。
(3)　ＢＧ：ＧＦは　　　：　　　です。






  左図で、三角形ＡＢＥの面積は１５、三角形ＢＣＥの面積は１０、三角形ＡＥＣの面積は５です。
(1)　ＢＤ：ＤＣ　を求めなさい。
(2)　ＡＥ：ＥＤ　を求めなさい。


問題４の答え(1)　３：１　　　　(2)　２：１
解説 　　　　  1/13

左図のように、長さの比が
５：２
であったとき、
どの面積の比も５：２になるでしょうか。考えてみてください。
補充問題(　　のところにマウスを近づけると、答えが表示されます。)

左図で、三角形ＡＢＥの面積は１２、三角形ＢＣＥの面積は１０、三角形ＡＥＣの面積は３です。
(1)　ＢＤ：ＤＣは、　　　：　　　です。
(2)　ＡＥ：ＥＤは、　　　：　　　です。






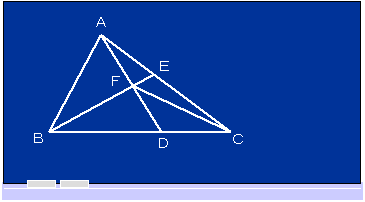  左図の三角形ＡＢＣで、ＢＤ：ＤＣ＝３：２、ＡＥ：ＥＣ＝３：４　です。
(1)　三角形ＡＢＦ、三角形ＢＣＦ、三角形ＡＦＣの面積の比を求めなさい。
(2)　ＡＦ：ＦＤ　を求めなさい。


問題５の答え(1)　３：４：２　　　　(2)　５：４
解説 　　　　  1/9

まず、問題に書いてあった比を、図に書きこんでおきましょう。
補充問題(　　のところにマウスを近づけると、答えが表示されます。)

左図の三角形ＡＢＣで、ＢＤ：ＤＣ＝３：２、ＡＥ：ＥＣ＝１：２　です。
(1)　三角形ＡＢＦ、三角形ＢＣＦ、三角形ＡＦＣの面積の比は、　　　：　　　：　　　です。
(2)　ＡＦ：ＦＤは、　　　：　　　です。